El casco de la nave es otro de los componentes cruciales para el rendimiento y funcionalidad de un vehículo submarino autónomo (AUV por sus siglas en inglés). Y en el caso del AUV AI-APAEC, su casco no solo debe cumplir con requisitos de resistencia y durabilidad, sino que también debemos optimizar la hidrodinámica y permitir el alojamiento de los sistemas internos necesarios para su autonomía. En esta iteración profundizaremos en el diseño del casco de un AUV, específicamente, en el diseño del casco del AI-APAEC.
Dentro del capítulo de diseño mecánico de un casco de un AUV, podríamos enfocarnos en muchos aspectos y requerimientos clave que delimitan el desarrollo de este componente, pero, en este proyecto, vamos a enfocarnos específicamente a los siguientes requerimientos:
- Hidrodinámica: Un diseño aerodinámico reduce la resistencia del agua, optimizando el consumo energético y prolongando la autonomía del vehículo. El perfil del casco debe minimizar la turbulencia y garantizar un flujo laminar.
- Resistencia a la presión: A medida que el AUV desciende a mayores profundidades, experimenta presiones hidrostáticas elevadas. Esto exige que el casco sea lo suficientemente resistente para evitar deformaciones o fallas estructurales.
- Integración de sensores y sistemas: El casco debe permitir la colocación estratégica de sensores, cámaras, antenas y otros dispositivos sin comprometer su eficiencia o estructura.
- Materiales ligeros y resistentes: Los materiales como las aleaciones de aluminio, fibra de carbono o composites son ideales para un casco resistente y liviano, lo que mejora tanto la flotabilidad como la maniobrabilidad.
Hidrodinámica del casco del AUV
La hidrodinámica del casco de un vehículo submarino autónomo (AUV) es un aspecto esencial que determina el rendimiento y eficiencia energética de la unidad en su entorno submarino. Un diseño hidrodinámico eficiente permite reducir la resistencia del agua al avance del AUV, mejorando su velocidad, maniobrabilidad y autonomía operativa. Habíamos mencionado que en esta iteración, nos íbamos a enfocar en el diseño del casco y vamos a empezar ahondando en las características hidrodinámicas del casco del AUV AI APAEC y cómo estas influyen en su rendimiento.
Un casco puede ser dividido en 3 secciones definidas como, la nariz, el cuerpo y la cola. El diseño fue basado en las Ecuaciones de Myring [1], que se sabe que producen una fuerza de arrastre mínima. Las formas de las secciones de la nariz y cola se determinan a partir de (1) y (2), respectivamente:
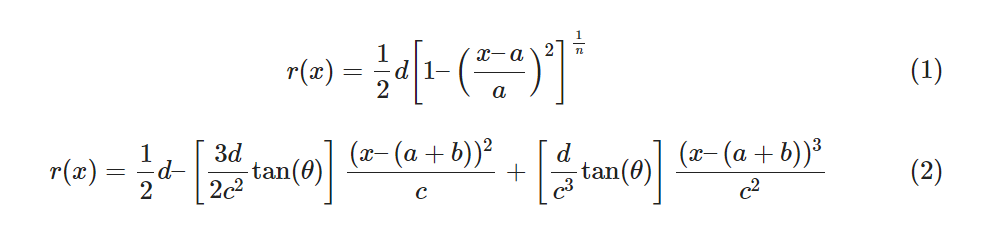
Donde \(r(x)\) es el radio en el punto \(x\) a lo largo del eje x, \(a\), \(b\) y \(c\) son las longitudes de la nariz, cuerpo y cola, respectivamente, \(d\) es el diámetro máximo, \(n\) es un parámetro exponencial que se puede variar para dar diferentes formas a la nariz y \(\theta\) es el ángulo de salida en la cola.
Para una definición precisa del casco del AI APAEC, es esencial establecer los valores específicos de los parámetros utilizados en las Ecuaciones de Myring. Los valores asignados son los siguientes:
- \(a=300mm\), longitud de la nariz
- \(b=900mm\), longitud del cuerpo
- \(c=200mm\), longitud de la cola
- \(d=180mm\), diámetro máximo
- \(n=2.5\)
- \(\theta=50°\)
Con estos valores, se puede definir la forma del casco en las secciones de la nariz y la cola utilizando las ecuaciones (1) y (2) mencionadas anteriormente. La elección de estas dimensiones no solo es fundamental para la hidrodinámica, sino que también se ha optimizado para asegurar que el AUV mantenga su estabilidad y eficiencia energética en diversas profundidades operativas.
Implementación del Modelo del Casco con Python
Una vez definidos los valores de los parámetros mencionados, procedemos a utilizar un script en Python para calcular las coordenadas de la curva del casco del AUV AI-APAEC. Esta curva se generó para posteriormente crear un sólido de revolución en Autodesk Inventor. A continuación, se presenta el script utilizado:
import numpy as np
import ezdxf
a = 300
b = 900
c = 200
d = 180
l = a+b+c
n = 2.5
theta = 50
theta = theta * np.pi / 180
x = np.linspace(0, l, 100)
body = np.zeros((len(x), 3))
values =[]
for count, element in enumerate(x):
if element <= a:
value = 0.5*d*(1-((element-a)/a)((element-a)/a))*(1/n)
if (element <= (a+b)) & (element > a):
value = d*0.5
if (element <= l) & (element > (a+b)):
value = 0.5*d - (3*d/(2*c*c)-np.tan(theta)/c)(element-a-b)(element-a-b) + (
d/(c*c*c)-np.tan(theta)/(c*c))(element-a-b)(element-a-b)*(element-a-b)
body[count] = np.array([x[count], value, 0])
doc=ezdxf.new('R2010')
msp=doc.modelspace()
msp.add_spline(body)
# save the DXF document
doc.saveas("spline30_degrees.dxf")Una vez que se han definido los valores de los parámetros y se ha ejecutado el script en Python, obtenemos un archivo DXF que contiene la curva del casco del AUV AI-APAEC. Este archivo puede ser importado fácilmente en un sketch de programas de diseño asistido por computadora como Autodesk Inventor o Fusion 360. De hecho, también es posible utilizarlo en SolidWorks. Al generar un sólido de revolución a partir de esta curva, se crea automáticamente la geometría del casco del AUV, lo que nos permite visualizar el diseño. Este flujo de trabajo asegura que se cumplan los requisitos hidrodinámicos, optimizando así el rendimiento del vehículo submarino.
Resultados del script
Después de ejecutar el script en Python, obtenemos como resultado un archivo en formato DXF que contiene la curva que define el perfil del casco del AUV AI-APAEC. Esta curva representa la geometría precisa del casco, calculada a partir de las ecuaciones de Myring, que están diseñadas para minimizar la resistencia hidrodinámica.


La capacidad de crear un modelo tridimensional a partir de un script automatizado no solo ahorra tiempo en la fase de diseño, sino que también reduce errores y permite iterar más rápidamente en la mejora del diseño del AUV.
Aquí te muestro el sólido de revolución ya generado. Además, dejo algunas capturas de pantalla del procedimiento que seguí.

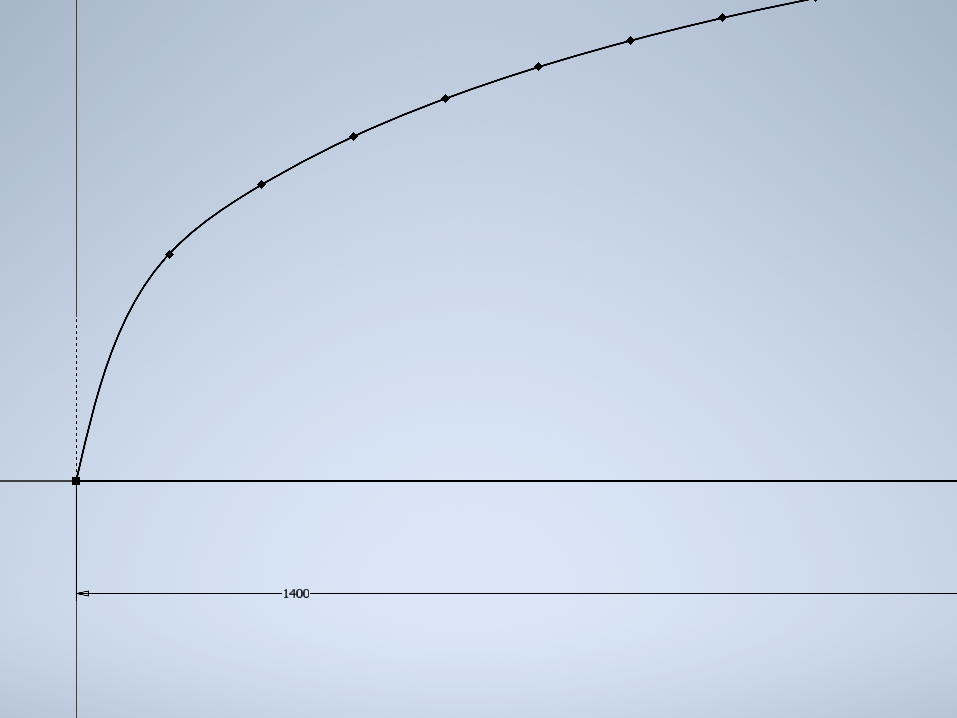
Es importante que en la punta de la nariz la curva sea tangente al plano frontal del vehículo. Así aseguramos que la nariz ‘rompe’ el agua con eficiencia.
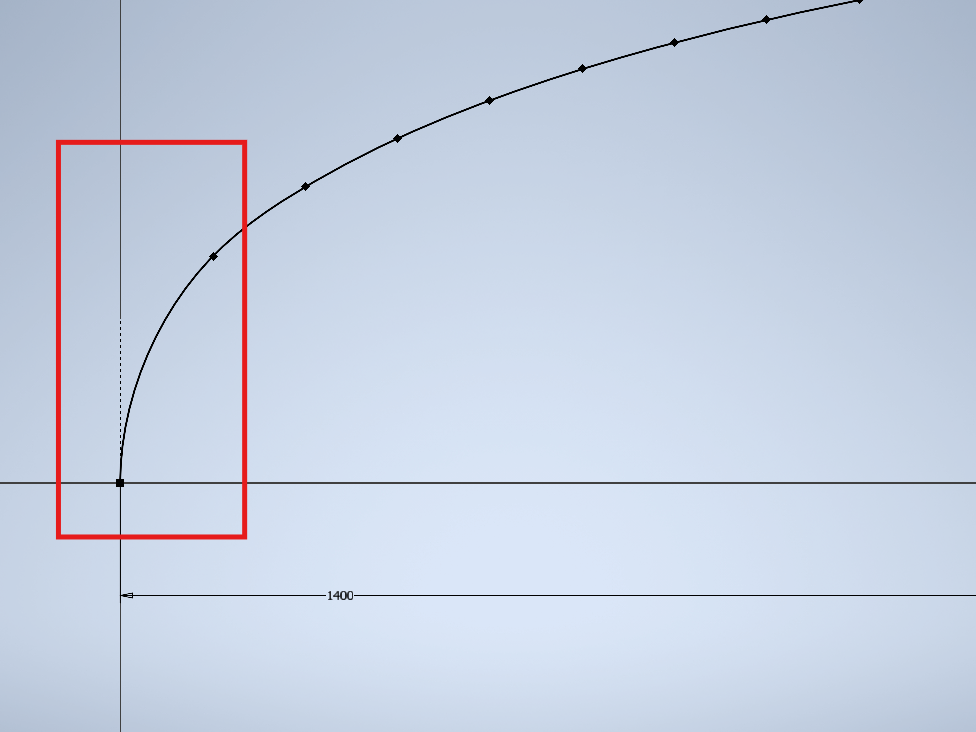
Finalizamos con la operación de revolución que va a generar el casco del AUV. Utilizando este sólido podemos realizar otras operaciones para terminar de diseñar y crear el casco del vehículo.
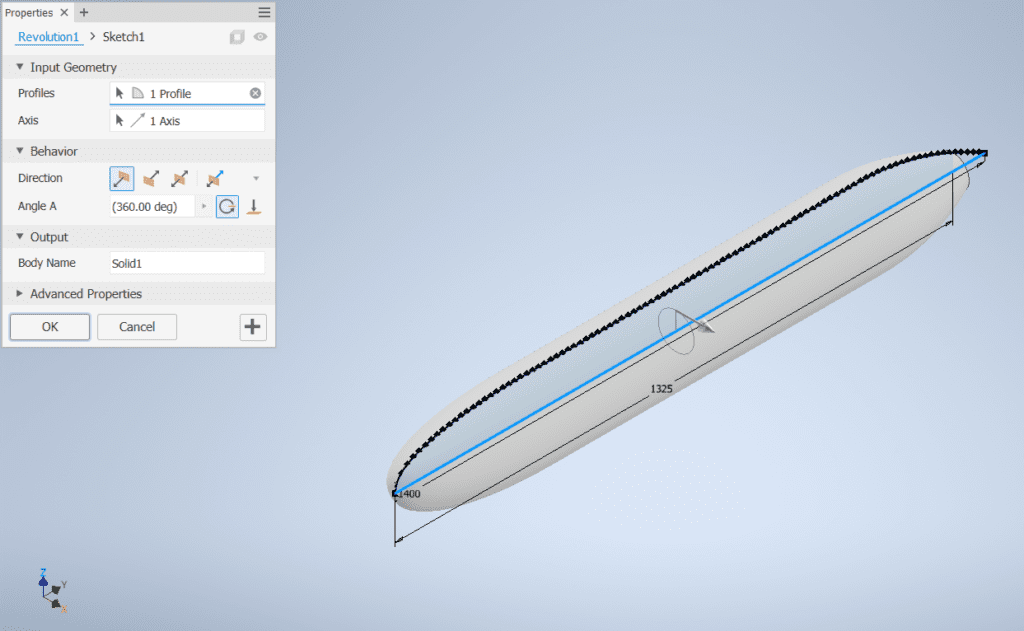
No es mi intención mostrar cada paso que he seguido para crear el diseño del AI-APAEC, esta parte del diseño lo dejo a libertad del lector.
Conclusiones
El diseño del casco del AUV AI-APAEC ha sido optimizado en términos de hidrodinámica mediante el uso de las ecuaciones de Myring y un poco de programación básica. Este proceso, que incluye la generación de un perfil en Python y la creación de un sólido de revolución en software CAD, garantiza precisión y eficiencia en el desarrollo del casco, y de la misma forma hemos reducido la resistencia, optimizando el consumo energético del AUV.
En la próxima iteración empezaremos a definir aspectos importantes sobre el diseño interno del AUV y además mostraré el modelo 3D del vehículo donde habremos integrado los propulsores que desarrollamos en la Iteración No. 1.
Bibliografía
- Myring, D. F.. A Theoretical Study of Body Drag in Subcritical Axisymmetric Flow. Aeronautical Quarterly, 1976. Volumen 27(3), pp. 186--194. DOI: 10.1017/s000192590000768x. URL: https://doi.org/10.1017/S000192590000768X.

